【数值分析课程实验-02】数值积分与微分

实验目标

使用编程语言实现以下算法：
1. 使用 复化梯形公式 的 自动控制误差 算法；
2. 使用 龙贝格积分 算法。
实现某个区间 [a, b] 上的积分：$I=\int_a^b{f\left( x \right) dx}$

编程语言与扩展库

编程语言：C++ 语言
IDE 环境：Visual Studio 2017
扩展库：Eigen 库

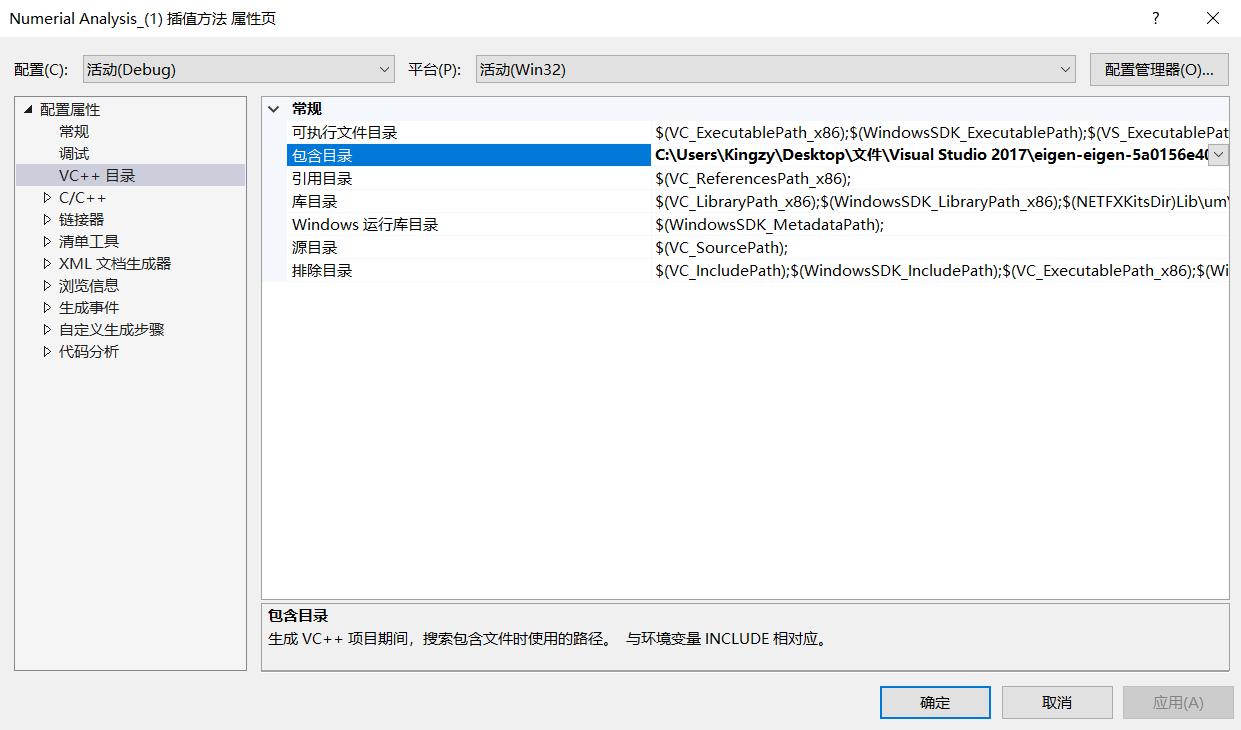
在项目名称处 右键 >> 属性 >> VC++目录 >> 包含目录 >> 选择 Eigen 模块所在文件夹路径，导入模块；
Eigen 资源文件可以在 Eigen 官网上进行下载。

实现代码

复化梯形积分

// 梯形法递推算法
// 参数：区间 [a,b]，误差阈值 w
void Trapezoid(double a, double b, double w)
{
	double h = b - a;    // h 代表步长
	double T1, T2, S;    // T1，T2 代表积分值，S 代表内切分点函数值总和
	double x;    // x 代表除区间边界外的内切分点
	int k = 0;    // 计数器
	
	T1 = 0.5*h*(f(a) + f(b));

	// 循环，直到误差足够小
	while (true) {
		// 打印迭代过程
		cout << "T" << pow(2, k) << " = " << T1 << endl;

		// 初始化
		x = a + 0.5*h;
		S = 0;

		// 将各切分点的函数值累加至累加 S
		while (x < b) {
			S += f(x);
			x += h;
		}

		// 计算出切分点增多后的积分值 T2
		T2 = 0.5*T1 + 0.5*h*S;

		// 如果误差足够小，跳出循环
		if (abs(T2 - T1) < w) break;
		// 如果误差较大，各区间再对半切分
		else {
			h = 0.5*h;
			T1 = T2;
			// 计数器自增
			k++;
		}
	}

	// 打印最终结果
	cout << endl << "最终计算结果：" << endl << "T = " << T2 << endl;
}

计算公式：

$$T_n=h\left( \frac{1}{2}f\left( a \right) +\sum_{i=1}^n{f\left( a+ih \right) +\frac{1}{2}f\left( b \right)} \right)$$

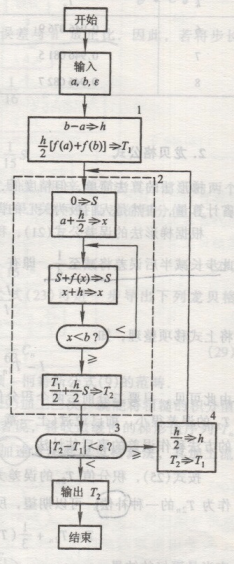
算法流程图：

龙贝格算法

// 龙贝格积分算法
// 参数：区间边界 [a,b]，误差阈值 w
void Romberg(double a, double b, double w)
{
	double h = b - a;
	double S, x;           
	
	// 计数器
	int k = 1;               

	// 梯形、辛普森、科特斯、龙贝格公式
	double T1, T2;  double S1, S2;
	double C1, C2;  double R1, R2;

	T1 = 0.5*h*(f(a) + f(b));
	cout << "T1 = " << T1 << endl;

	// 循环，直到误差足够小
	while (true) {
		// 初始化
		x = a + 0.5*h;
		S = 0;

		// 将各切分点的函数值累加至累加 S
		while (x < b) {
			S += f(x);
			x += h;
		}

		T2 = 0.5*T1 + 0.5*h*S;
		cout << "T" << pow(2, k) << " = " << T2 << endl;

		// 梯形公式外推辛普森公式
		S2 = T2 + (T2 - T1) / 3;
		cout << "S" << pow(2, k - 1) << " = " << S2 << endl;

		if (k == 1) {
			// 步长对半
			k += 1;  h = 0.5*h;
			T1 = T2;  S1 = S2;
		}
		else {
			// 辛普森公式外推科特斯公式
			C2 = S2 + (S2 - S2) / 15;
			cout << "C" << pow(2, k - 2) << " = " << C2 << endl;

			if (k == 2) {
				C1 = C2;
				// 步长对半
				k += 1;  h = 0.5*h;
				T1 = T2;  S1 = S2;
			}
			else {
				// 科特斯公式外推龙贝格公式
				R2 = C2 + (C2 - C1) / 63;
				cout << "R" << pow(2, k - 3) << " = " << R2 << endl;

				if (k == 3) {
					R1 = R2;
					C1 = C2;
					// 步长对半
					k += 1;  h = 0.5*h;
					T1 = T2;  S1 = S2;
				}
				else {
					if (abs(R2 - R1) < w) break;
					else {
						R1 = R2;
						C1 = C2;
						// 步长对半
						k += 1;  h = 0.5*h;
						T1 = T2;  S1 = S2;
					}
				}
			}
		}
	}

	// 打印最终结果
	cout << endl << "最终计算结果：" << endl << "R = " << R2 << endl;
} 

算法流程图：

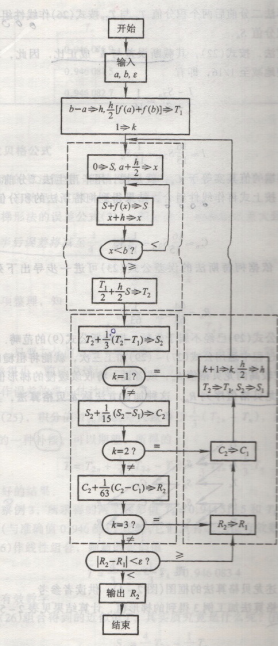
源代码整合

#include <Eigen/Dense>
#include <iostream>
#include <fstream>
#include <vector>
#include <cmath>

using namespace Eigen;
using namespace std;

// 积分函数  f(x) = sin(x)/x
double f(double x)
{
	if (x == 0) return 1;
	else return sin(x) / x;
}

// 梯形法递推算法
// 参数：区间 [a,b]，误差阈值 w
void Trapezoid(double a, double b, double w)
{
	double h = b - a;    // h 代表步长
	double T1, T2, S;    // T1，T2 代表积分值，S 代表内切分点函数值总和
	double x;    // x 代表除区间边界外的内切分点
	int k = 0;    // 计数器
	
	T1 = 0.5*h*(f(a) + f(b));

	// 循环，直到误差足够小
	while (true) {
		// 打印迭代过程
		cout << "T" << pow(2, k) << " = " << T1 << endl;

		// 初始化
		x = a + 0.5*h;
		S = 0;

		// 将各切分点的函数值累加至累加 S
		while (x < b) {
			S += f(x);
			x += h;
		}

		// 计算出切分点增多后的积分值 T2
		T2 = 0.5*T1 + 0.5*h*S;

		// 如果误差足够小，跳出循环
		if (abs(T2 - T1) < w) break;
		// 如果误差较大，各区间再对半切分
		else {
			h = 0.5*h;
			T1 = T2;
			// 计数器自增
			k++;
		}
	}

	// 打印最终结果
	cout << endl << "最终计算结果：" << endl << "T = " << T2 << endl;
}

// 龙贝格积分算法
// 参数：区间边界 [a,b]，误差阈值 w
void Romberg(double a, double b, double w)
{
	double h = b - a;
	double S, x;           
	
	// 计数器
	int k = 1;               

	// 梯形、辛普森、科特斯、龙贝格公式
	double T1, T2;  double S1, S2;
	double C1, C2;  double R1, R2;

	T1 = 0.5*h*(f(a) + f(b));
	cout << "T1 = " << T1 << endl;

	// 循环，直到误差足够小
	while (true) {
		// 初始化
		x = a + 0.5*h;
		S = 0;

		// 将各切分点的函数值累加至累加 S
		while (x < b) {
			S += f(x);
			x += h;
		}

		T2 = 0.5*T1 + 0.5*h*S;
		cout << "T" << pow(2, k) << " = " << T2 << endl;

		// 梯形公式外推辛普森公式
		S2 = T2 + (T2 - T1) / 3;
		cout << "S" << pow(2, k - 1) << " = " << S2 << endl;

		if (k == 1) {
			// 步长对半
			k += 1;  h = 0.5*h;
			T1 = T2;  S1 = S2;
		}
		else {
			// 辛普森公式外推科特斯公式
			C2 = S2 + (S2 - S2) / 15;
			cout << "C" << pow(2, k - 2) << " = " << C2 << endl;

			if (k == 2) {
				C1 = C2;
				// 步长对半
				k += 1;  h = 0.5*h;
				T1 = T2;  S1 = S2;
			}
			else {
				// 科特斯公式外推龙贝格公式
				R2 = C2 + (C2 - C1) / 63;
				cout << "R" << pow(2, k - 3) << " = " << R2 << endl;

				if (k == 3) {
					R1 = R2;
					C1 = C2;
					// 步长对半
					k += 1;  h = 0.5*h;
					T1 = T2;  S1 = S2;
				}
				else {
					if (abs(R2 - R1) < w) break;
					else {
						R1 = R2;
						C1 = C2;
						// 步长对半
						k += 1;  h = 0.5*h;
						T1 = T2;  S1 = S2;
					}
				}
			}
		}
	}

	// 打印最终结果
	cout << endl << "最终计算结果：" << endl << "R = " << R2 << endl;
} 

int main()
{
	// 复化梯形算法
	cout << endl << "复化梯形算法：" << endl;
	Trapezoid(0, 1, 1e-6);

	// 龙贝格算法
	cout << endl << "龙贝格算法：" << endl;
	Romberg(0, 1, 1e-6);

	return 0;
}

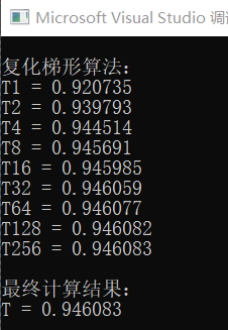
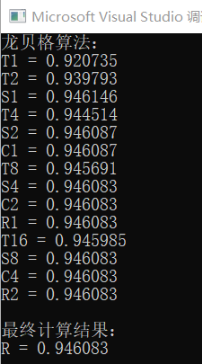
运行结果

程序选择 $f\left( x \right) =\sin \left( x \right) /x$ 作为积分函数，计算其 $\left[ 0,\ 1 \right]$ 上的积分值。

写在最后

声明：本专栏内容来源于武汉理工大学 2019-2020 学年数值分析方法课程实验，仅供学习参考。
如有错误或不足地方，还请指出，祝愿读者能够在编程之路上不断进步！